0
Submit

DATA STRUCTURES


Data Structures Tutorial


Admission Enquiry Form

Binary Tree

The binary tree is a kind of tree in which almost two children can be found for each parent. A parent in binary tree can have one, two or none children, but it can't have more than two children.



Properties of Binary tree

  1. Minimum number of nodes in a binary tree of height H = H + 1
  2. Maximum number of nodes in a binary tree of height H = 2H+1 – 1
  3. Total Number of leaf nodes in a Binary Tree = Total Number of nodes with 2

    children + 1
  4. Maximum number of nodes at any level ‘L’ in a binary tree = 2L


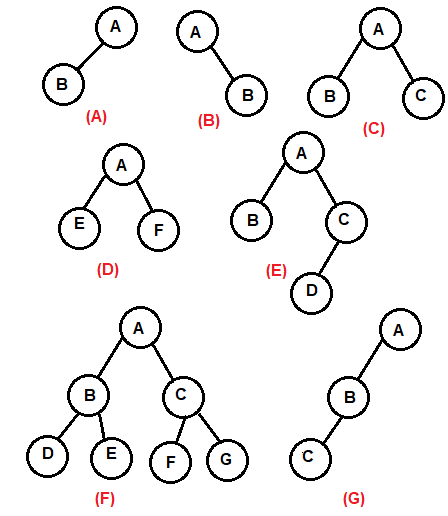
Examples of Binary Trees



Types of Binary tree

  1. Full/Strict/Proper Binary Tree
  2. Complete Binary Tree
  3. Perfect Binary Tree


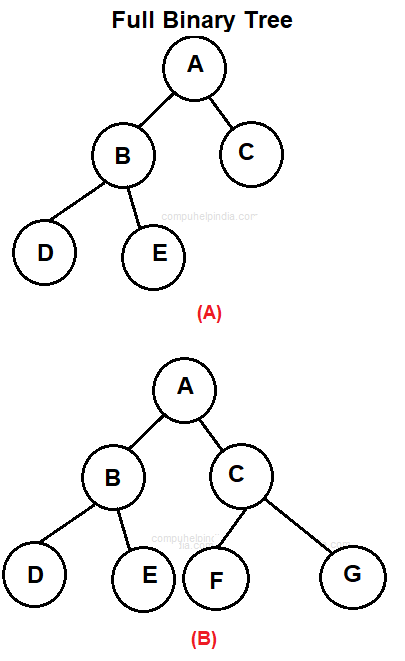
Full/Strict/Proper Binary tree

A binary tree is a Full binary tree if each node has exactly zero or two children.



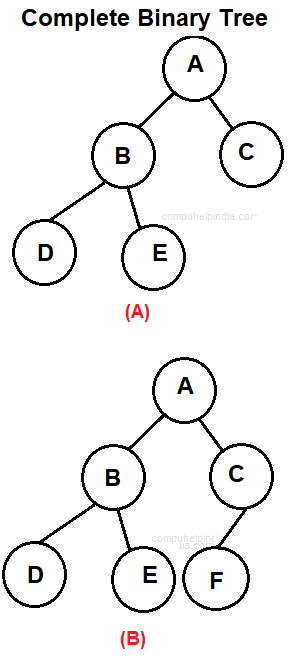
Complete Binary tree

A binary tree is a Complete binary tree which is either a full binary tree or one in which every level is fully occupied except possibly for the bottommost level where all the nodes must be as far left as possible.



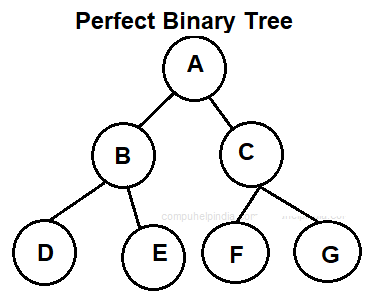
Perfect Binary tree

A binary tree is a Perfect binary tree when its all internal nodes have two children and all leaves are at same level.