0
Submit

DATA STRUCTURES


Data Structures Tutorial


Admission Enquiry Form

Memory Representation of Binary Tree

A number of different representations can be used for binary trees depending upon how you setup the link between nodes and its children.A binary tree can be represented in memory either using an array or linked list.



Array Representation of Binary tree

In the array representation of binary tree, we store the nodes of a binary tree in an array level by level, left to right starting from the root node till all the leaf nodes are stored.

The size of the array TREE can be determined using the property of binary tree according to which a binary tree of height h can have atmost 2h+1-1 nodes.Therefore, the size of array tree is 2h+1-1.



Examples of Binary Trees

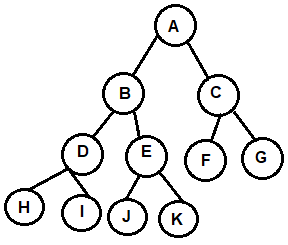
We can store the nodes of binary tree as follows:

  1. The root node A will be stored at index 1 i.e. at TREE[1].


Types of Binary tree

  1. Full/Strict/Proper Binary Tree
  2. Complete Binary Tree
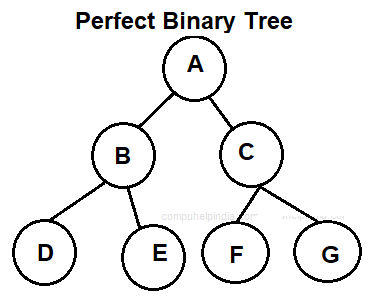
  3. Perfect Binary Tree


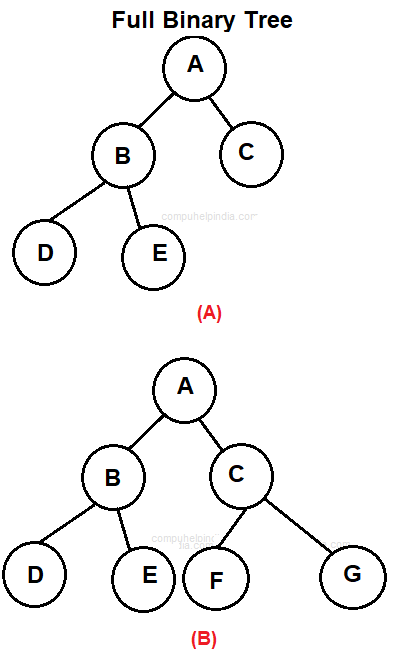
Full/Strict/Proper Binary tree

A binary tree is a Full binary tree if each node has exactly zero or two children.



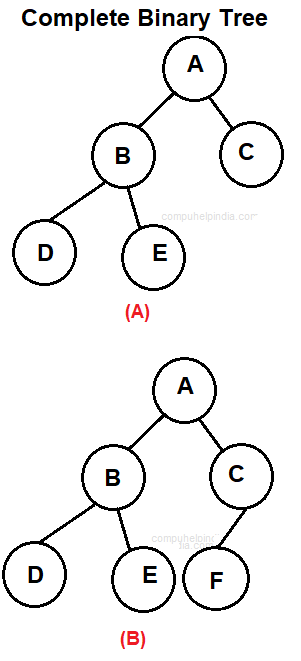
Complete Binary tree

A binary tree is a Complete binary tree which is either a full binary tree or one in which every level is fully occupied except possibly for the bottommost level where all the nodes must be as far left as possible.



Perfect Binary tree

A binary tree is a Perfect binary tree when its all internal nodes have two children and all leaves are at same level.